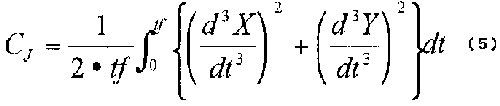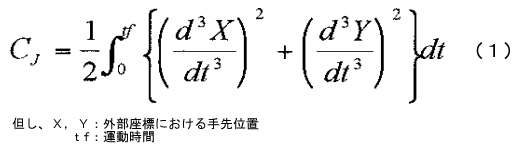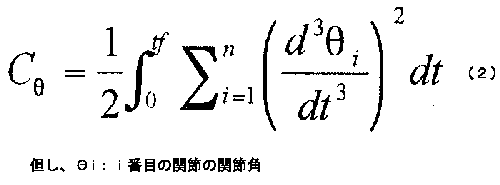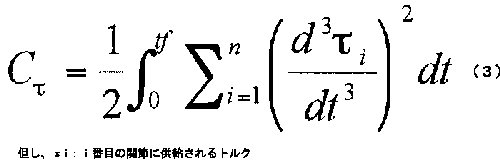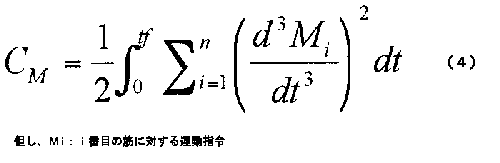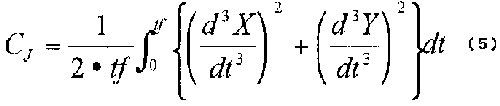随意運動の運動計画規範
指示動作は、手指で指示棒を握り、対象となるシンボルを指し示す動作であり、これは、手部が指示棒の分だけ延長された上肢についての手先位置制御課題として解釈することができる。
腕の多関節運動による手先位置制御課題について、軌道計画の規模としては、手先直交座標躍度最小(以下、「手先躍度最小」),関節角躍度最小,トルク変化最小,運動指令変化最小などの評価関数が提案されている。
最適化理論に基づいた運動計画では、何らかの規範に基づいており、その評価関数を最適化(最小化)する形で軌道を生成するものと思われる。
したがって、最適化されている軌道に比べて、最適化されていない軌道は、採用されている評価関数の値が大きくなるはずであり、そこから仮説として、評価関数の値の大小により、運動が最適化されているかそうでないか、言い換えれば、自然な動きかそうでないかを評価できると思われる。
その評価関数として、実際の生体がどのような規範を採用しているかはここでは議論せず、近似的な評価関数を採用することにより評価を行う。
手先位置制御についての規範と評価関数を以下に示す。
(1)手先躍度最小規範
躍度とは、位置の時間に関する3階微分であり、躍度最小とは、加速度の変化が小さい、すなわちなめらかな動きであることを示す。
この規範の評価関数は式(1)である。
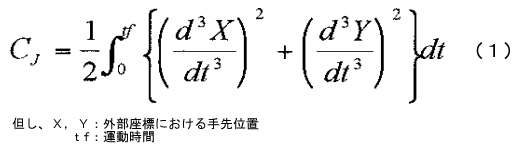
(2)関節角躍度最小規範
この規範では、関節角空間での躍度を評価する。
この規範の評価関数は式(2)である。
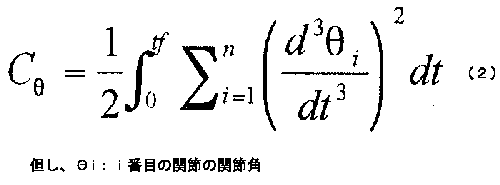
(3)トルク変化最小規範
この規範は、トルクが時間的にもっとも滑らかに変化するように軌道を計画する。
この規範の評価関数は式(3)である。
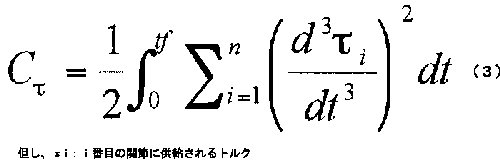
(4)運動指令変化最小規範
この規範では、末梢ではなく中枢神経系における滑らかさを拘束条件とし、時間的に激しく変化しない運動指令を作り出すことを意味する。
運動指令として最も末梢に近いレベルでは、i番目の筋に達する全ての神経インパルスの総和として定められる。
運動指令を求めるに当たっては、筋電図から筋レベルでの運動指令を推定する方法がとられることがある。
この規範の評価関数は式(4)である。
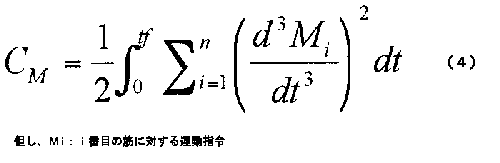
手先躍度最小規範に基づくモデルもさまざまな条件下で運動をよく再現することが知られている(またはオリジナル)。
手先躍度最小規範は評価関数が視覚の作業座標のみで与えられ、神経筋骨格系のダイナミックスは反映されない。
また特に、手先躍度最小規範は元来、外力のない自由な運動に関する規範であり、指示動作のような鉛直平面での手先位置制御のような重力が作用する運動では、手先躍度最小規範は適用が困難である。
したがって、ヒトの水平面内での手先位置制御については、手先躍度最小規範は不適切であり、運動指令最小規範が妥当な結果を与える傾向にあることが知られている。
しかしながら本研究では、より簡便な測定方法を得るために、規範の第一近似として手先躍度最小規範を採用する。
指示動作に対する手先躍度最小評価については、手先の座標、すなわち指示棒先端の座標が必要である。
この測定については、3章で述べた視聴者モデルのポインタ軌跡推定ブロックを用いることができる。
この座標データを式(1)に従って計算することで、指示動作中の評価関数が得られる。
但し、動作時間について規格化するため、実際には式(5)を採用する。