|


概要
関数解析学は、古典解析に対して現代解析とも呼ばれ、種々の、数学または応用上の問題を、バナッハ空間や関数空間とその上の作用素などの現代的手法を用いて研究するものです。
特に、工学や自然科学の多くの分野で、関数空間とその上の作用素の問題として定式化される例が多くあります。我々は、ここ十数年、関数空間とその上の作用素の基礎的研究をしています。さらに、最近は4年次卒業研究でフラクタルの基礎研究を始めています。
1.非有界微分と関数空間
このテ−マは、物理学の量子統計力学の基礎づけについての理論的研究から生じた問題の特別な場合で、連続関数空間上の非有界微分の定義空間上の等距離作用素の構造を決定すること、さらに一般に荷重合成作用素の性質について明らかにすることが中心になります。
2.関数空間上の線形汎関数および作用素の摂動に対する安定性の研究
このテ−マは、数学以外の分野とも関係が深く、種々の関数空間上の作用素を摂動した場合、どれだけその性質が変わるかを摂動の大きさを用いて精密に評価することが目標です。
以上の他に次のようなテ−マについても研究を始めています。
3.フラクタルの基礎研究
フラクタルは、自然界の地形、金属表面の凹凸、結晶成長、細菌のコロニ−成長パタ−ンなど不規則・複雑な形や現象のことで、数学、自然科学、工学の多くの分野にまたがる研究対象です。現在4年次卒業研究において、主としてコンピュ−タシミュレ−ションによって、フラクタル次元、ランダムフラクタル図形の生成とその応用を中心とした研究を進めています。
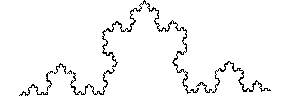
コッホ曲線

コッホ曲線の確率的変形による海岸線のモデル
(H14年度研究室4年次生卒業論文 海津・渡辺・森田「ランダムフラクタル図形の生成」より) |